Теплопроводность
Известно, что процесс распространения теплоты в пространстве неразрывно связан с распределением температуры в нем. Совокупность значений температуры в каждый момент времени для всех точек рассматриваемого пространства называется температурным полем. Математически оно выражается уравнением t = f (х, у, z, τ), где х, у, z - координаты точки, а т - время. Если температура во времени не меняется, то поле называется установившимся, или стационарным. Если температура зависит от времени, поле называется неустановившимся, а протекающие в таких условиях тепловые процессы - нестационарными, например нагревание или охлаждение тел.
Температурное поле может быть функцией трех, двух и одной координаты. Соответственно оно называется трех, двух - и одномерным. Наиболее простой вид имеет уравнение одномерного стационарного температурного поля t = f (х). Все точки пространства, имеющие одинаковую температуру, образуют изотермическую поверхность. Естественно, что изменение температуры в теле может наблюдаться лищь в направлениях, пересекающих изотермические поверхности (например, направление х, рис. 13.1). При этом наиболее резкое изменение получается в направлении нормали n к изотермическим поверхностям. Предел отношения изменения температуры Δt к расстоянию между изотермами по нормали Δn при условии, что Δn = 0, называется температурным градиентом, т.е.
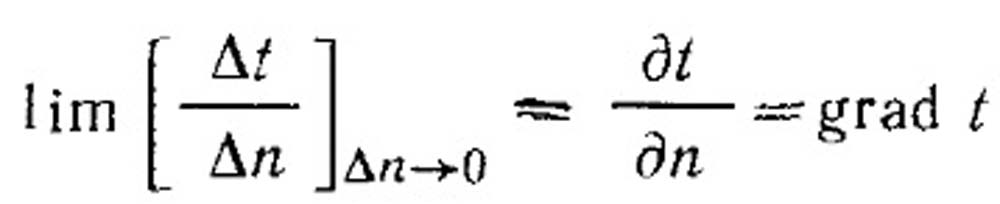
Частная производная применена здесь потому, что в общем случае температура может изменяться не только в пространстве, но и во времени (при нестационарном режиме).
Температурный градиент - это вектор с положительным знаком при возрастании температуры и с отрицательным при ее падении. Градиент температуры численно равен производной температуры по нормали.
Количество переносимой теплоты в единицу времени называют тепловым потоком Q, который измеряется в Дж/с (Вт). Тепловой поток, отнесенный в единице поверхности тела, называют по верхностной плотностью теплового потока (или просто плотностью теплового потока) q = Q/S, которая измеряется в Вт/м2.
Величина q является вектором, направление которого противоположно направлению градиента температуры, так как тепловая энергия самостоятельно распространяется всегда только в сторону убывания температуры (см.рис. 13.1).
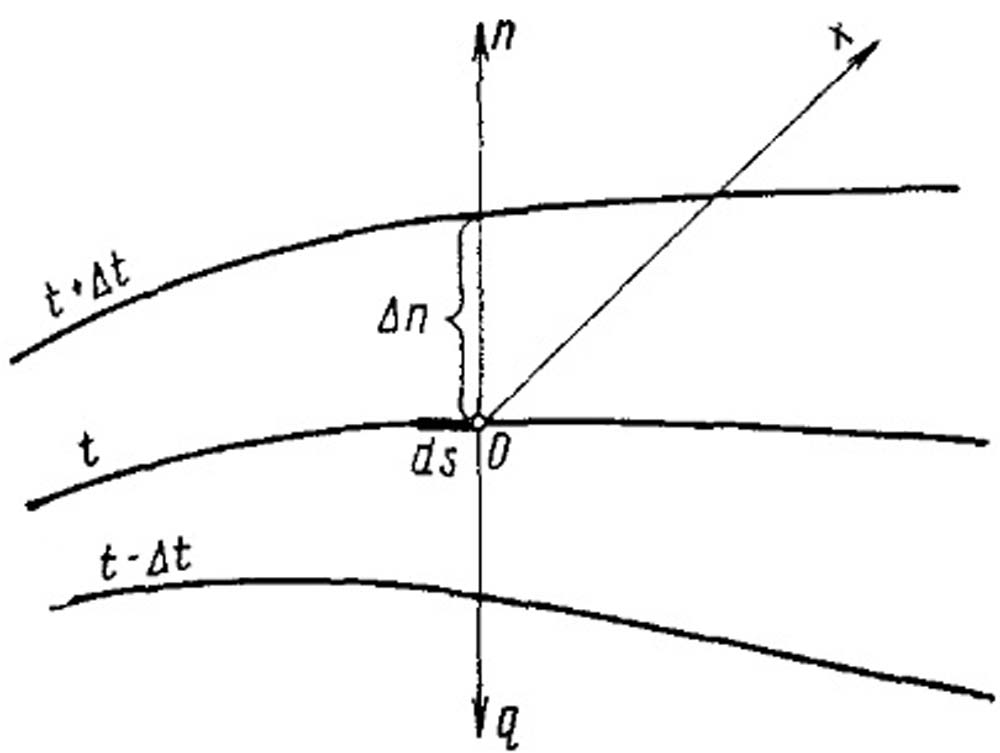
Рис. 13.1. К определению температурного градиента и теплового потока.
Исследуя явления теплопроводности в твердых телах, Фурье установил, что тепловая мощность, тока передаваемая теплопроводностью, пропорциональна градиенту температуры пендикулярного направлению теплового потока, т. е.
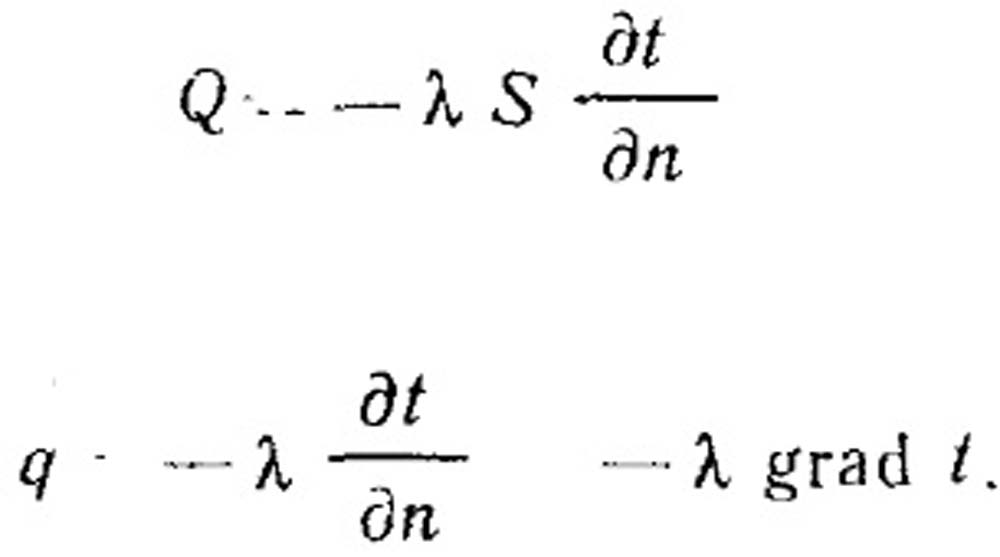(13.1)
Множитель пропорциональности λ, входящий в это уравнение, характеризует способность вещества, из которою состоит рассматриваемое тело, проводить теплоту и называется коэффициентом теплопроводности, или просто теплопроводностью. Из уравнения (13.1), которое является математическим выражением основного закона распространения теплоты путем теплопроводности (закон Фурье), следует, что теплопроводность λ, Вт/(м×К), определяет мощность теплового потока, проходящего через 1 м2 поверхности при градиенте температуры 1 К/м.
Для различных тел теплопроводность имеет определенное значение и зависит от структуры, плотности, влажности, давления и температуры веществ этих тел. Точные значения λ определяют на основе специальных лабораторных опытов. При технических расчетах обычно используют ориентировочные значения теплопроводности λ, Вт/(м×К).
Таким образом, наиболее высокая теплопроводность у металлов, значительно ниже у неметаллических строительных материалов и самые низкие значения у пористых материалов, применяемых специально для тепловой изоляции. У теплоизоляционных материалов λ < 0,20 Вт/(м × К).
У большинства металлов с повышением температуры теплопроводность убывает. Содержание примесей в металлах резко снижает их теплопроводность. Например, для стали при 0,1% углерода λ = 53, а при 1% углерода λ = 39 Вт/(м × К). Для строительных и теплоизоляционных материалов теплопроводность возрастает с увеличением температуры (исключение составляют магнезитовые огнеупоры). Зависимость λ от температуры для этих материалов может быть выражена равенством:
λ1 - λ0 °С(1 + βt)
где β - температурный коэффициент, представляющий собой приращение λ материала при повышении его температуры на 1°.
У различных строительных материалов в интервале температур 0 - 100° С β = 0,0025. Для капельных жидкостей с повышением температуры теплопроводность убывает. Исключение составляют лишь вода и глицерин. У газов с повышением температуры теплопроводность возрастает и практически не зависит от давления, за исключением очень высоких (более 200 МПа) и очень низких (менее 0,003 МПа) давлений. На теплопроводность влияют общая пористость материала, размер и степень замкнутости пор. Для пористых материалов теплопроводность находится в обратной зависимости от их общей пористости и в прямой от размеров пор. Это объясняется увеличением передачи теплоты конвекцией и излучением в общем процессе теплообмена пористого материала и свидетельствует о том, что теплоизоляционные материалы, используемые при высоких температурах, должны иметь мелкопористое строение. Поры, сообщающиеся между собой и с поверхностью материала, создают более благоприятные условия для увлажнения материала и тем самым для увеличения его теплопроводности, поэтому теплоизоляционные материалы должны иметь по возможности замкнутые поры.
Для пористых материалов λ является условной величиной, так как наличие пор в материале не позволяет рассматривать его как сплошное тело. Поэтому λ пористых материалов представляет собой теплопроводность некоторого однородного тела, через которое при одинаковых форме, размерах и температурах на границе его поверхности с окружающей средой передается та же тепловая мощность, что и через пористое тело.
Материалы с большей плотностью, как правило, обладают большей теплопроводностью, однако нужно иметь в виду, что теплопроводные свойства материала зависят не только от объема воздуха, заключенного в порах, но главным образом от равномерного распределения воздуха в пористом материале. С этой точки зрения крупнопористый материал будет менее эффективным теплоизолятором, чем мелкопористый материал с той же плотностью. Среди строительных материалов встречаются такие, которые, имея меньшую плотность, обладают большей теплопроводностью, чем материалы с большей плотностью. Примерами могут служить минеральная вата, торфяная крошка, употребляемая в качестве теплоизоляционного сыпучего материала, и др. В частности, в минеральной ваты при плотности около 125 кг/м3 теплопроводность наименьшая. При меньшей плотности теплопроводность возрастает в результате увеличения передачи теплоты конвекцией в порах вследствие меньшего уплотнения ваты.
Теплопроводность строительных материалов резко возрастает при их увлажнении, так как значительно отличаются теплопроводности воздуха и воды: теплопроводность воздуха в порах материала 0,025 - 0,028, а воды 0,55 Вт/(м×К), т. е. почти в 20 раз больше, чем воздуха. Материал становится еще более теплопроводным, если влага, находящаяся в его порах, замерзает, так как теплопроводность льда равна 2,5 Вт/(м×К), т. е. примерное 4 раза выше, чем у воды, и в 80 раз выше, чем у воздуха. Повышение теплопроводности влажных материалов обусловливается также увеличением контактирующих поверхностей частиц основного вещества материала. Это приводит к тому, что теплопроводность влажного материала значительно выше, чем сухого и воды в отдельности. Например, для сухого кирпича λ равна 0,35, для воды 0,55, а для влажного кирпича 1 Вт/(м×К) Поэтому строительные и особенно теплоизоляционные материалы необходимо предохранять от увлажнения, иначе сильно снижаются их теплозащитные свойства.
Для анизотропных материалов, которые имеют неодинаковую структуру в различных направлениях (древесина, волокнистые и прессованные материалы, кристаллы), теплопроводность зависит от направления теплового потока. Например, у сосновой древесины при направлении теплового потока параллельно направлению волокон увеличивается вдвое по сравнению с теплопроводностью при направлении теплового потока перпендикулярно волокнам. Это объясняется тем, что при направлении, перпендикулярном волокнам, тепловому потоку приходится пересекать большое количество воздушных зазоров, находящихся как внутри волокон древесины, так и между ними и оказывающих сопротивление прохождению теплоты. При направлении теплового потока параллельно волокнам влияние воздуха, заключенного в древесине, будет значительно меньше.